C.2 (I numeri irrazionali quadratici e le) frazioni continue
Si tratta di un percorso condotto al Liceo Buonarroti in una classe seconda; è un ulteriore esempio dei possibili sviluppi dell'argomento sulle frazioni.
Prima fase
Nella prima fase si scopre come ogni frazione possa essere scritta come 'frazione continua', cioè un numero intero più l'inverso di... un numero intero più l'inverso di... fino a trovare, dopo un numero finito di passaggi, un numero intero più l'inverso di un numero intero.
Esempio:
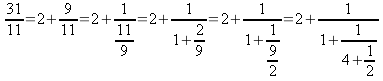
Applicando l'algoritmo euclideo ai numeri 31 e 11 si ottiene:
| 1° numero |
2° numero |
quoziente |
resto |
| 31 |
11 |
2 |
9 |
| 11 |
9 |
1 |
2 |
| 9 |
2 |
4 |
1 |
E' chiaro il legame tra quozienti e resti delle divisioni successive nell'algoritmo euclideo applicato ai numeri 31 e 11, e i numeri che compaiono nella rappresentazione in frazione continua di 31/11.
Alla frazione 31/11 si associa la terna (2;1;4) dei quozienti delle divisioni successive; ad ogni frazione corrisponde una frazione continua finita; viceversa, a partire da una lista ordinata (finita) di numeri si può costruire una frazione continua e quindi una frazione corrispondente.
Seconda fase.
Nella seconda fase si ricostruisce una frazione partendo da una lista finita di numeri e passando attraverso la frazione continua individuata da tale lista; si eslpora anche il comportamento di frazioni equivalenti rispetto alle corrispondenti frazioni continue.
Terza fase
Nella terza fase si indaga sulla possibilità di esprimere radicali quadratici con frazioni continue. Per esempio,
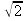 , che è compresa tra 1 e 2, si può
scrivere come
, che è compresa tra 1 e 2, si può
scrivere come 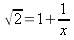 ; risolvendo,
risulta che
; risolvendo,
risulta che 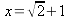 ; dunque l'equazione
diventa:
; dunque l'equazione
diventa: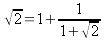 ,
,da cui si capisce il suo
carattere periodico, e lo sviluppo in frazione continua (illimitata)
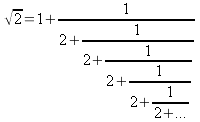
Sostituendo 1/2 ai puntini dopo diversi passaggi, gli studenti trovano approssimazioni per difetto e per eccesso di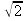 .
.
Quarta fase.
Ai ragazzi è stato proposto di trovare la frazione continua relativa a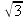 ; il procedimento
è più complesso e porta ad una rappresentazione periodica
del tipo
; il procedimento
è più complesso e porta ad una rappresentazione periodica
del tipo
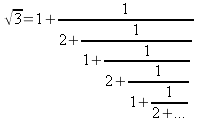 .
.
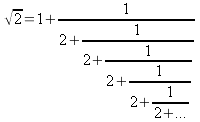
Sostituendo 1/2 ai puntini dopo diversi passaggi, gli studenti trovano approssimazioni per difetto e per eccesso di
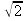 .
.Quarta fase.
Ai ragazzi è stato proposto di trovare la frazione continua relativa a
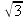 ; il procedimento
è più complesso e porta ad una rappresentazione periodica
del tipo
; il procedimento
è più complesso e porta ad una rappresentazione periodica
del tipo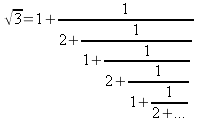 .
.Quinta fase.
Vengono infine proposte frazioni continue costruite a partire da equazioni di secondo grado complete, sostituendo all'equazione
Vengono infine proposte frazioni continue costruite a partire da equazioni di secondo grado complete, sostituendo all'equazione
x2+bx+c=0
In particolare è stata studiata l'equazione della sezione
aurea, (si considera a=1) quella
equivalente
x=b+c/x.
x2=x+1;
le frazioni continue 'ridotte',
approssimazioni della soluzione, forniscono il rapporto tra un numero
di Fibonacci eil suo precedente, e quindi forniscono tutti i nuemri di
Fibonacci.
Tutta l'attività è descritta nella presentazione allegata.
Tutta l'attività è descritta nella presentazione allegata.