A]
Proposte elaborate dal gruppo di lavoro 'per cominciare' con le frazioni
A.1] Frazioni e numeri decimali
A.2]
Il Tangram
A.3]
L'algoritmo euclideo: dal massimo comun divisore alla misura delle
grandezze.
A.1]
Frazioni e numeri decimali
Su questo tema c'è un percorso
didattico completo nella pubblicazione Matematica 2003 dell'UMI.
Quelli che seguono sono quesiti tratti liberamente da questo documento
ed altri elaborati dal gruppo.
1. Di che tipo sono i numeri decimali
associati alle frazioni?
Descrivili.
Si prevede un utilizzo abbastanza libero del
linguaggio. Utilizzando il
programma
Javascript allegato, gli allievi provano diversi casi e osservano
le prime regolarità: i
decimali vengono quasi sempre periodici, e in certi casi finiti.
2. Quando i numeri decimali
vengono periodici e quando finiti?
Controlla i dati in ingresso e scopri in che relazione sono con il tipo
di risultato.
Ci si aspettano delle ipotesi, e delle
confutazioni. Non ci si
aspettano dimostrazioni complete. Viene stimolato l'uso del linguaggio
per verbalizzare le 'regole' ipotizzate.
3. Ma siamo proprio sicuri?
Si mette in dubbio quanto ipotizzato
proponendo esempi particolari,
come 1/49 o 1/343 (si veda a questo proposito l'approfondimento
disciplinare sulle
frazioni). Gli allievi sono stimolati ad aumentare il numero
delle cifre richieste per controllare la loro congettura (quella che
venga un numero decimale sempre periodico); [notiamo che in questo
momento noi
facciamo delle congetture sulle loro risposte, e quindi interroghiamo,
non osserviamo, la realtà]. Sono stimolati a trovare una ragione
di quanto accade.
4. (Parte centrale) Ma il
viceversa vale? Cioè, partendo da un
numero finito o periodico, esiste sempre una frazione corrispondente?
Si evita di chiamarla 'generatrice' per tenere
lontano dalla mente la
'regola' meccanica, spesso già appresa. Prima o poi viene fuori,
confusa. Bisogna cercare
di lavorare sul fatto che è difficile ricordarla, che è
facile confondersi, forse non vale la pena ricordarla; proviamo a
ragionarci su...
Un tentativo: 0,(3)=0,3+0,0(3), cioè
0,3 + 1/10 del numero
stesso... cioè 0,(3) supera di 0,3 la sua decima parte... (frase
tipica di molti 'problemi'...) vuol dire che i 9/10 di 0,(3) sono
uguali al numero stesso privato del periodo... quindi, moltiplicando
0,3 per 10/9 si ottiene il numero periodico... scritto in una forma in
cui il periodo non c'è più; e 0,3 corrisponde a una
frazione? (Propedeutico).
L'attività così impostata
ricorda molto il lavorare con
una 'cosa', una 'x' se vogliamo. E' come un'equazione; è un po'
più astratta di un'equazione, perché non si cerca un
'valore' (infatti 0,(3) è già dato), ma una 'forma'
voluta.
Affrontare queste domande costituisce già un percorso completo
sull'argomento; altri quesiti individuati dal Gruppo di lavoro, da
utilizzarsi anche per un'eventuale prova d'ingresso, sono i seguenti:
5. Trovare l'n-esima cifra
decimale del numero corrispondente a una
frazione data
Per esempio, la centesima cifra di
1/7=0,(142857); poiché il periodo di 1/7 ha lunghezza 6, dopo 96
cifre si ripete il periodo: dunque la centesima cifra è uguale
alla quarta, cioè 8.
6. Qual è la frazione
ridotta associata a 0,(9) ?
La non univocità della scrittura decimale di
un numero è un argomento che lascia dubbi perfino negli adulti
esperti, come risulta da alcuni questionari rivolti a laureati in
materie scientifiche; piuttosto che 'imporre' una soluzione, è
probabilmente più utile una discussione in classe.
7. Calcola l'espressione:
(0,(142857)+0,(2(142857))x(9,(3)-0,8(3)-0,(27))x0,(285714).
Quando è stato proposto questo
esercizio, molti alunni sono passati spontaneamente alla
forma frazionaria, riconoscendone l'utilità.
8. La calcolatrice ha sempre
ragione? Calcolare (1/7)x8-1; che cosa
succede iterando il procedimento? Perché?
A causa di una propagazione degli errori di
approssimazione nei passi
successivi, la calcolatrice dopo un certo numero di passaggi fornisce
risultati divergenti, e quindi palesemente errati. Una utile
discussione sulla differenza tra calcolo esatto e approssimato.
9. (Domanda 4 del MAT2003): Data una frazione ridotta, come si
determina il numero di cifre della parte decimale che precede il
periodo (antiperiodo) nel numero decimale corrispondente?
Un modo per
'testare' se e quanto i ragazzi sono coinvolti nel gioco e disposti a
fare
propri dei problemi ormai molto specifici.
A.2] Il Tangram
Abbiamo strutturato questa proposta di attività in varie fasi,
lasciando aperte alcune possibilità in merito ad approfondimenti
ed obiettivi possibili; ad esempio, nella fase 2 è prevista la
costruzione del Tangram. A seconda degli strumenti utilizzati,
l'attività può essere semplice, quasi ludica (come con la
piegatura della carta), oppure gradatamente più difficile, e con
obiettivi più specifici di tipo geometrico (ad es. con software
dinamico opportunamente calibrato nel menù), oppure può
aprire la possibilità di un percorso completo di geometria
euclidea: basta porsi il
problema di costruire un quadrato con riga e compasso, e chiedersi perché il quadrilatero
ottenuto è proprio un quadrato, e si ricostruisce molta della
geometria assoluta, fino al teorema delle parallele. Per ogni fase
abbiamo indicato le competenze sollecitate nella sua realizzazione (non
quelle in uscita, ma quelle attivate per affrontare l'attività).
Fase 1 (preliminare, anche per prova d'ingresso).
- Chiedere di spiegare come si costruisce un quadrato con una
o più delle modalità della fase 2.
Per rendere 'sensato' il problema occorre
escludere la carta a quadretti: i ragazzi devono spiegare come si
costruisce un quadrato su un foglio bianco o su uno schermo del
computer privo di riferimenti geometrici (griglie, assi...).
- In quanti modi si può dividere un quadrato in due
parti uguali?
Certamente i ragazzi avranno diversi modi,
forse molto somiglianti fra loro, per fare questa divisione; da una
discussione dovrebbero accorgersi che questi modi sono in realtà
infiniti. L'attività in sé può concludersi qui, ma
è 'generativa' di molte idee che possono essere sviluppate
successivamente. Tante 'metà' del quadrato, di tante forme
diverse, dovranno avere necessariamente la stessa 'superficie' (il
termine è usato in senso intuitivo). Otteniamo così
poligoni 'equiestesi' anche se non esplicitamente equiscomposti. Un
buon inizio per affrontare, in tempi successivi, l'argomento
dell'equivalenza tra equiscomposizione ed equiestensione dei poligoni.
Fase 2: costruire il Tangram seguendo delle istruzioni
con varie
modalità:
- con piegatura della carta
- con software dinamico (Geogebra,
Euclidian, GeoLabo, Declic, Cabri, Kig, DrGeo,...).
- con
riga e compasso (partendo da un quadrato o costruendo il
quadrato)
Competenze
sollecitate: questa consegna
richiede ed esercita la capacità di servirsi del linguaggio matematico
finalizzata ad uno scopo operativo e la coordinazione oculo-manuale per
l'esecuzione del compito.
Fase 2: Tagliare i singoli pezzi del
Tangram e riconoscere quale
frazione dell'intero ogni pezzo rappresenta; lavorare per equivalenza sia in senso numerico
(frazioni equivalenti) sia in senso geometrico (equivalenza di
superfici); ordinare in
entrambi i significati (riconoscere che la 'contenenza' è
condizione sufficiente ma non necessaria per l'ordinamento
dell'estensione). Spingersi anche in problemi di calcoli di perimetri
(fissando un'unità di misura) e confrontare l'isoperimetria con l'equiestesione.
Competenze sollecitate: saper riconoscere
rapporti geometrici; saper classificare
ed ordinare rispetto ad un
criterio dato.
Fase 3: (eventuale) una
proposta nell'ottica del Cooperative
Learning: costruire
puzzle
in gruppo; i pezzi vengono suddivisi tra i componenti del gruppo
e
ognuno può toccare solo i suoi; gli elementi del gruppo possono
tuttavia comunicare per suggerire come sistemare i pezzi. Per i puzzle esiste un software scaricabile
liberamente che permette di costruire figure, coi pezzi del
tangram, a tre livelli di difficoltà.
Competenze sollecitate: saper lavorare
in squadra rispettando regole
e ruoli. Competenza comunicativa e relazionale, assunta esercitando
atteggiamenti cooperativi e non competitivi (vedi "Cooperative Learning").
A.3]
L'algoritmo euclideo: dal massimo comun divisore alla misura delle
grandezze.
Una parte degli Elementi di Euclide, meno conosciuta
del celeberrimo primo libro,
riguarda l'aritmetica (libro VII), e il legame di questa con la teoria
delle grandezze (libro V). Contrariamente a quanto certi pregiudizi
potrebbero far credere, è proprio questo approccio antico quello
che meglio si presta ad una visione algoritmica e costruttiva
dell'aritmetica, adatta anche per l'elaborazione al computer. Il
massimo comun divisore tra due numeri non viene introdotto tramite la
fattorizzazione, come di consueto, ma con un algoritmo, detto appunto euclideo, che si
basa sulle divisioni successive. Euclide si serve dello stesso
algoritmo per definire i rapporti tra grandezze (e quindi la misura di
una grandezza rispetto ad un'altra, presa come unità),
estendendolo dal caso commensurabile a quello incommensurabile. Il
percorso nella sua interezza è adatto ad una fase di revisione
critica dell'aritmetica (triennio liceale), ma le prime
attività, che proponiamo, sono stimolanti, non difficili, e
legate a molta parte della matematica, in particolare dell'algebra,
anche moderna. Abbiamo segnalato come opzionali quelle attività
che più si avvicinano alla visione 'superiore' dell'intero
argomento.
Fase
1 -
Esplorazione: Dare coppie di numeri e assegnare il compito seguente:
togliendo successivamente il minore dal maggiore che cosa si ottiene?
Provando con molte coppie, scelte a caso dai ragazzi singolamente o per
gruppi, si giunge a congetturare che si ottenga il Massimo Comun
Divisore; sarà vero? E se è vero, perché?
Non è possibile
(nel senso che è molto
improbabile) che si giunga ad una dimostrazione della congettura;
tuttavia le discussioni alimentano la necessità di approfondire.
Fase 2 - Formalizzazione: Analizzare che
cosa succede all'insieme dei
divisori comuni sostituendo la coppia (a;b), con a>b, la coppia
(a-b; b). Perché avviene questo?
Gli studenti si
accorgono che l'insieme dei divisori
comuni non cambia, per esempio rappresentando gli insiemi dei divisori
di a e di b, e considerando la loro intersezione; si possono utilizzare
diagrammi di Venn o rappresentazioni per elencazione. Ma parché
avviene questo?
Senza entrare in
formalismi inutilmente complicati,
al 'cuore' del funzionamento dell'algoritmo euclideo c'è solo la
proprietà distributiva,
in questo caso della moltiplicazione rispetto alla sottrazione.
Indichiamo con la notazione "x|y" le locuzioni equivalenti
- x divide y
- x è divisore
di y
- y è multiplo
di x
Dimostriamo
che l'insieme dei divisori comuni
della coppia (a;b), con a>b,
è lo stesso della coppia
(a-b; b); infatti, se d|a e d|b, allora (per la distributiva della
moltiplicazione rispetto alla sottrazione) d|a-b; viceversa, se
d|a-b e d|b, allora (per la distributiva della moltiplicazione rispetto
all'addizione) d|a-b+b, cioè d|a.
Fase 3 - Applicazione dell'algoritmo:
velocizzare l'algoritmo delle
sottrazioni successive con le divisoni successive (algoritmo euclideo)
e applicarlo a numeri "grandi".
Si 'riscopre' il
significato di divisione con
resto come 'sottrazione ripetuta finché si può'; a questo
punto diviene opportuno l'utilizzo della calclatrice; è un
utilizzo non banale; per esempio, per calcolare il MCD tra 10767 e
5322, occorre riconoscere il quoziente intero, che in questo caso
è 2, e, applicando la definizione, calcolare il resto della
divisione: 10767-2x5322=123; ma
MCD(10767;5322)=MCD(5322;123);
..........................................
si ripete l'algoritmo (divisione
di 5322 per 123 per calcolare il quoziente intero, calcolo del resto,
ecc.), fino a trovare il MCD, che è 3.
Gli studenti possono
apprezzare la
potenzialità e l'efficacia dell'algoritmo, con cui si possono
trattare coppie di numeri ben più alte di quelle con cui si ha
in genere a che fare con
il metodo (decisamente inefficiente) della fattorizzazione.
Fase 3 - Esplorazione: Che cosa succede
applicando la procedura delle
sottrazioni successive ad una coppia di frazioni?
Senza ricercare una
formalizzazione completa, si scopre che si ottiene sempre una frazione
che ha al numeratore il MCD dei numeratori e al denominatore il mcm dei
denominatori. Le due frazioni risultano multipli interi primi tra loro
della frazione trovata. L'esperienza ha un profondo significato
geometrico: se due grandezze sono commensurabili, l'algoritmo euclideo
individua la massima grandezza che 'misura' le prime due, nel senso
euclideo; si trova cioè la massima grandezza sottomultipla
comune delle due grandezze date. Nel caso dei numeri interi, c'è
comunque una grandezza unica che le misura tutte: è
l'unità.
Fase 3bis (opzionale) - Rivisitazione del
concetto intuitivo di
grandezza acquisito nella scuola media. Che cosa è una classe di
grandezze; che cosa è il rapporto tra due grandezze e la misura
di una grandezza; possibilità di calcolare una misura con
l'algoritmo di Euclide (per le grandezze commensurabili).
L'argomento delle
grandezze viene generalmente proposto
(quando non viene 'saltato' a pié pari) all'inizio del secondo
anno del biennio; si tratta di un capitolo
spesso difficile, anche per l'insegnante, in quanto il linguaggio
proposto nei testi è generalmente in bilico tra quello antico di
Euclide e quello moderno di Hilbert, per giungere al concetto di numero
reale, quello moderno, formalizzato solo alla fine dell'800. D'altra
parte, ci sono approcci che prevedono l'introduzione dei
numeri reali (in senso inutitivo) fin dal primo anno. In questo senso
abbiamo pensato a questa fase dell'attività come opzionale per
il primo anno. Seguire il linguaggio
euclideo, senza pretenderne il rigore, restituisce coerenza e chiarezza
all'argomento, e, ricalcando il loro ordine storico, aiuta a
comprendere gli sviluppi successivi.
Le grandezze per
Euclide sono semplicemente oggetti
che si possono confrontare e sommare, indipendentemente dalla
loro natura; in questo riconosciamo nell'Autore una visione della
matematica molto vicina a quella moderna, di tipo strutturale. E se, date due grandezze A e B,
risulta A>B, allora postuliamo che esista una grandezza C, che
chiameremo A-B, tale
che B+C=A. Ma quante volte dovremo sommare la grandezza B
per raggiungere A? Forse tante... l'importante è che siano in
numero finito, cioè che esista un numero intero n tale che
nB>A (Assioma di Archimede); è questo che permette la
'divisione euclidea' tra grandezze e quindi la possibilità di
parlare di rapporto, definendolo tramite l'algoritmo euclideo;
l'algoritmo euclideo infatti nel caso di grandezze incommensurabili
fornisce la massima grandezza sottomultipla comune D, tale che A=mD e
B=nD, cosicché vale la proporzione A:B=m:n, cioè il
numero razionale m/n è il rapporto
tra A e B, ovvero la misura
di A rispetto a B. Per il caso incommensurabile è utile
l'attività seguente, che può essere proposta anche
indipendentemente da questa formalizzazione.
Fase 4 - Esplorazione: Che
cosa succede applicando la procedura delle sottrazioni successive
a 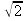 e 1?
Senza pretendere una
formalizzazione completa, si
scopre che il
procedimento non ha termine, ma che si ottengono numeri via via
più piccoli, espressi come combinazioni lineari, a coefficienti
interi discordi via via più grandi, di
e 1?
Senza pretendere una
formalizzazione completa, si
scopre che il
procedimento non ha termine, ma che si ottengono numeri via via
più piccoli, espressi come combinazioni lineari, a coefficienti
interi discordi via via più grandi, di 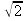 e
di 1; il rapporto
tra i coefficienti interi delle
combinazioni lineari ottenute fornisce un'approssimazione via via
migliore di
e
di 1; il rapporto
tra i coefficienti interi delle
combinazioni lineari ottenute fornisce un'approssimazione via via
migliore di 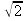 ;
la successione dei numeri che si ottengono
dalle sottrazioni successive rappresenta lo 'scarto' tra il valore di
;
la successione dei numeri che si ottengono
dalle sottrazioni successive rappresenta lo 'scarto' tra il valore di 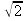 e le sue approssimazioni razionali.
Fase 4bis (opzionale) - Formalizzazione
mediante interpretazione
geometrica; il procedimento delle sottrazioni successive corrisponde ad
una costruzione geometrica che si autoriproduce, pertanto non ha
termine. Grandezze incommensurabili.
e le sue approssimazioni razionali.
Fase 4bis (opzionale) - Formalizzazione
mediante interpretazione
geometrica; il procedimento delle sottrazioni successive corrisponde ad
una costruzione geometrica che si autoriproduce, pertanto non ha
termine. Grandezze incommensurabili.
Fase 5 - Formalizzazione di tipo aritmetico - La radice quadrata di 2
è un numero irrazionale.
Si può porre in discussione la dimostrazione classica, con o
senza
ragionamento per assurdo; si può decidere se rendere più
o meno esplicito l'utilizzo (che viene effettivamente fatto) del
teorema fondamentale dell'aritmetica. In particolare, discutere in
classe perché è
impossibile l'uguaglianza tra
numeri interi
m2=2n2
(indipendentemente dal fatto di scegliere
m ed n primi tra loro) è un'ottima occasione per cogliere il
significato di tale teorema, che viene ormai ritenuto scontato a causa
del lungo addestramento a scomporre i numeri in fattori primi.
Fase 5bis (opzionale) - Il teorema fondamentale dell'aritmetica,
scoperta guidata: esistenza e unicità della scomposizione in
fattori primi.
L'esistenza di una scomposizione di fattori primi può essere
data per scontata,
così come lo era per Euclide (la dimostrazione sarebbe
troppo formale); basta far osservare, con dei diagrammi ad albero, che
la definizione di numero composto comporta una diramazione in due
fattori, e così via... e che i numeri diventano via via
più piccoli. Per
l'unicità, i diversi
diagrammi ad albero costruiti dai ragazzi
mostrano l'unicità del risultato finale. E'
assai sconsigliabile
la scomposizione mediante lo schema della linea verticale e
l'applicazione dei criteri di divisibilità ai possibili fattori
primi in ordine crescente, proprio perché così non viene
messa in luce l'unicità della scomposizione. L'unicità
può essere parzialmente formalizzata grazie al lemma seguente:
"Se un numero primo divide un prodotto, allora divide almeno uno dei
fattori".
di
facile dimostrazione con l'uso di frazioni: se p|ab, allora esiste d
tale che pd=ab, quindi vale l'uguaglianza di frazioni p/a=b/d. Se p|a
non c'è niente da dimostrare; se p non divide a, allora la
frazione p/a è ridotta ai minimi termini, quindi b e d sono
multipli, rispettivamente, di p ed a.
Fase
5ter (opzionale) - Le equazioni diofantee. Problema:
"Sarebbe possibile introdurre un
sistema monetario basato
soltanto su tagli di 3 e 5? Più specificatamente, quali valori
si otterrebbero su questa base? Sarebbe desiderabile un tale sistema,
se fosse possibile?"
Si tratta di un problema tratto dalla pubblicazione
[P], relativa allo studio OCSE-PISA sulla valutazione dei quindicenni
nei paesi dell'OCSE. Il problema, che si trova alla pagina 37 della
pubblicazione, viene commentato nel modo seguente: "è un buon
problema,
non tanto per la sua vicinanza al mondo reale, quanto per il fatto che
è interessante dal punto di vista matematico"; prosegue: "Il
ricorso
alla matematica per spiegare scenari ipotetici ed
esplorare sistemi o situazioni alternativi, anche se improbabili,
è una
delle caratteristiche più importanti di tale disciplina." In
effetti
introduce in modo estremamente semplice ad un fatto aritmetico molto
importante: la risolubilità sugli interi delle equazioni
diofantee, di
cui non è necessaria alcuna formalizzazione, ma la cui
esplorazione è
motivante e formativa, e fa appprezzare la matematica. E' interessante
notare come i ragazzi, discutendo tra loro, difficilmente trovino la
soluzione più semplice: dando due monete da tre e ricevendo una
moneta
da cinque di resto, si può 'scambiare' il valore unitario,
quindi tutti
i valori interi. Ma è anche interessante, proprio da queste
risposte,
apprezzare il fatto che le soluzioni per 'scambiare' il valore unitario
sono infinite, e le coppie, rappresentate sul piano cartesiano, danno
luogo a punti tutti allineati...
Riproporre il problema, cambiando i
tagli delle
monete, permette di rendersi
conto senza una eccessiva
formalizzazione che il
problema è risolubile solo prendendo coppie di numeri primi tra
loro. E' facile dimostrare la non risolubilità nel caso
contrario, con la proprietà distributiva, ma non la
risolubilità nel caso dei numeri primi tra loro, che però
può essere sperimentata in molti casi.
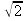 e 1?
e 1? 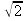 e
di 1; il rapporto
tra i coefficienti interi delle
combinazioni lineari ottenute fornisce un'approssimazione via via
migliore di
e
di 1; il rapporto
tra i coefficienti interi delle
combinazioni lineari ottenute fornisce un'approssimazione via via
migliore di 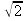 ;
la successione dei numeri che si ottengono
dalle sottrazioni successive rappresenta lo 'scarto' tra il valore di
;
la successione dei numeri che si ottengono
dalle sottrazioni successive rappresenta lo 'scarto' tra il valore di 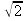 e le sue approssimazioni razionali.
e le sue approssimazioni razionali. 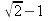 . Ma DF è la
diagonale del quadrato di lato ED; dunque, geometricamente, siamo
tornati al caso di partenza e possiamo ripetere indefinitamente i tre
passaggi.
. Ma DF è la
diagonale del quadrato di lato ED; dunque, geometricamente, siamo
tornati al caso di partenza e possiamo ripetere indefinitamente i tre
passaggi.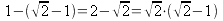 ; sono di nuovo due
numeri di rapporto
; sono di nuovo due
numeri di rapporto